Ikkilik sanoq sistemasi

Ikkilik sanoq sistemasi sonlarni faqat 2 belgi, 0 va 1 raqamlaridan foydalanib yozishga asoslangan sanoq tizimidir.

Razryad

Har qanday natural son uchun, har bir xona birligiga nisbatan, razryad(tartib) tushunchasi ishlatiladi. Yaʼni, birlar xonasida joylashgan son 0-razryad, oʻnlar xonasida joylashgan son 1-razryad, yuzlar xonasida joylashgan son 2-razryad va shu tarzda davom etadi.

Pozitsion yoyilma

Har qanday asosli sanoq sistemada qisqa yozuvda berilgan sonlarni asos(oʻnlik sanoq sistemasi uchun 10 soni olinadi, ikkilik sanoq sistemasi uchun 2 soni olinadi …) darajalari boʻyicha yoyib yozish mumkin va bu pozitsion yoyilma deb yuritiladi.

Masalan, oʻnlikk sanoq sistemasidagi $457_{10}$sonini $4\times 10^2+5\times 10^1+7\times 10^0$ kabi yozish mumkin. Bu yerda, 7 soni birlar xonasida joylashgan, yaʼni 0-razryadda joylashgan, shu sababli u $10^0$ soniga koʻpaytirilmoqda. 5 soni oʻnlar xonasida joylashgan, yaʼni 1-razryadda joylashgan, shu sababli u $10^1$ soniga koʻpaytirilmoqda va 4 soni yuzlar xonasida joylashgan, yaʼni 2-razryadda joylashgan, shu sababli u $10^2$ soniga koʻpaytirilmoqda. Odatda sonning quyi indeksiga qaysi sanoq sistemasida berilganligi yozib qoʻyiladi, masalan $457_{10}$ soni oʻnlik sanoq sistemasida berilganligini bildiradi.

Boshqa sanoq sistemalarida ham sonlar shu tarzda yoziladi. Masalan, ikkilik sanoq sistemasidagi $1011_2$ sonini quyidagicha yoyib yozish mumkin

$1011_2=1\times 2^3+0\times 2^2+1\times 2^1+1\times 2^0$

Berilgan sonni oʻnlik sanoq sistemasiga oʻtkazish uchun uni pozitsion yoyilmasini yozib, koʻpaytirish va qoʻshish amalini bajarish kifoya. Masalan,

$a)101_2=1\times 2^2+0\times 2^1+1\times 2^0=1\times 4+0\times 2+1\times 1=4+1=5_{10}$

$b)101011_2=1\times 2^5+0\times 2^4+1\times 2^3+0\times 2^2+1\times 2^1+1\times 2^0=32+8+2+1=43_{10}$

Oʻnlik sanoq sistemadan ikkilik sanoq sistemaga oʻtish

Oʻnlik sanoq sistemadan ixtiyoriy boshqa n lik sanoq sistemaga oʻtish uchun:

1. oʻnlik sanoq sistemadagi berilgan son n soniga burchakli boʻlish usulida boʻlinadi va qoldiq yozib olinadi.
2. keyingi qadamda hosil boʻlgan boʻlinma yana n soniga boʻlinadi,  . . .
3. bunda  boʻlish boʻlinma n sonidan kichik boʻlguniga qadar davom ettiriladi.
4. hosil boʻlgan boʻlinma va qoldiqlar ohiridan boshga qarab (pastdan tepaga qarab) yozib olinadi.

bu son biz izlagan javob boʻladi!

$$\begin{array}{cc}{O}^{\prime }nlikdagison& Ikkilikdagik{o}^{\prime }rinishi\\ 0& 0\\ 1& 1\\ 2& 10\\ 3& 11\\ 4& 100\\ 5& 101\\ 6& 110\\ 7& 111\\ 8& 1000\\ 9& 1001\\ 10& 1010\\ 11& 1011\\ 12& 1100\\ 13& 1101\\ 14& 1110\\ 15& 1111\end{array}$$

Masalan,

$a)19_{10}$ sonini ikkilik sanoq sistemasiga o‘tkazish

$b)235_{10}$ sonini ikkilik sanoq sistemasiga o‘tkazish

O'nlik sanoq sistemasida berilgan sonni ikkilik sanoq sistemasiga o'tkazish

$c)407_{10}$ sonini ikkilik sanoq sistemasiga o‘tkazish

Darajaga yoyish usuli

2 sonining darajalari

daraja (n)	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
qiymati (2^n)	1	2	4	8	16	32	64	128	256	512	1024	2048	4096	8192	16384	32768

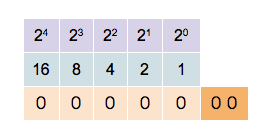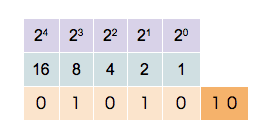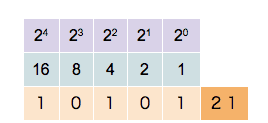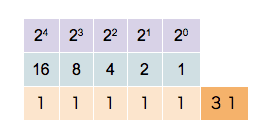
Shuningdek, oʻnlik sanoq sistemasida soni ikkilik sanoq sistemasiga oʻtkazishni darajaga yoyish usuli ham mavjud. Bu usulda oʻnlik sanoq sistemasida berilgan k sonini ikkining darajalari yigʻindisi koʻrinishida tasvirlanadi. Darajaga yoyib borishda, k sonidan katta boʻlmaydigan ikkining eng katta darajasi olinadi. Masalan,

$a)37_{10}$

$1)2^5\le 37<2^6$ bundan, $2^5$ni olamiz. Qolayotgan son: $37-2^5=37-32=5\ne 0$

$2)2^2\le 5<2^3$ bundan, $2^2$ni olamiz. Qolayotgan son: $5-2^2=5-4=1\ne 0$

$3)2^0\le 1<2^1$ bundan, $2^0$ni olamiz. Qolayotgan son: $1-2^0=1-1=0$ va jarayon tugadi.

demak, $37_{10}=32+4+1=2^5+2^2+2^0$ tarzida yoyilar ekan va bu sonni pozitsion yoyilma koʻrinishiga oʻtkazamiz. Bunda, ishtirok etmagan ikkining darajalari oldida nol koeffitsient bor deb olinadi. Yaʼni

$37_{10}=32+4+1=2^5+2^2+2^0=1\times 2^5+0\times 2^4+0\times 2^3+1\times 2^2+0\times 2^1+1\times 2^0.$

Endi, ikkining oldidagi koeffitsientlarni razryadiga mos tarzda, ketma-ket yozib olamiz $1\times 2^5+0\times 2^4+0\times 2^3+1\times 2^2+0\times 2^1+1\times 2^0\to 100101_2$

Yaʼni, $37_{10}=100101_2$

$b)98_{10}$

$1)2^6\le 98<2^7$ bundan, $2^6$ni olamiz. Qolayotgan son: $98-2^6=98-64=34\ne 0$

$2)2^5\le 34<2^6$ bundan, $2^5$ni olamiz. Qolayotgan son: $34-2^5=34-32=2\ne 0$

$3)2^1\le 2<2^2$ bundan, $2^1$ni olamiz. Qolayotgan son: $2-2^1=2-2=0$ va jarayon tugadi.

demak, $98_{10}=64+32+2=2^6+2^5+2^1$ tarzida yoyilar ekan va bu sonni pozitsion yoyilma koʻrinishiga oʻtkazamiz

$98_{10}=64+32+2=2^6+2^5+2^1=1\times 2^6+1\times +2^5+0\times 2^4+0\times 2^3+0\times 2^2+1\times 2^1+0\times 2^0$

va $1\times 2^6+1\times +2^5+0\times 2^4+0\times 2^3+0\times 2^2+1\times 2^1+0\times 2^0\to 1100010_2$

Yaʼni, $98_{10}=1100010_2$

$c)128_{10}$

$1)2^7\le 128<2^8$ bundan, $2^7$ni olamiz. Qolayotgan son: $128-2^7=128-128=0$ va jarayon tugadi.

demak, $128_{10}=2^7$ tarzida yoyilar ekan va bu sonni pozitsion yoyilma koʻrinishiga oʻtkazamiz

$128_{10}=2^7=1\times 2^7+0\times 2^6+0\times 2^5+0\times 2^4+0\times 2^3+0\times 2^2+0\times 2^1+0\times 2^0$

va $1\times 2^7+0\times 2^6+0\times 2^5+0\times 2^4+0\times 2^3+0\times 2^2+0\times 2^1+0\times 2^0\to 10000000_2$

Yaʼni, $128_{10}=10000000_2$

$d)63_{10}$

$1)2^5\le 63<2^6$ bundan, $2^5$ni olamiz. Qolayotgan son: $63-2^5=63-32=31\ne 0$

$2)2^4\le 31<2^5$ bundan, $2^4$ni olamiz. Qolayotgan son: $31-2^4=31-16=15\ne 0$

$3)2^3\le 15<2^4$ bundan, $2^3$ni olamiz. Qolayotgan son: $15-2^3=15-8=7\ne 0$

$4)2^2\le 7<2^3$ bundan, $2^2$ni olamiz. Qolayotgan son: $7-2^2=7-4=3\ne 0$

$5)2^1\le 3<2^2$ bundan, $2^1$ni olamiz. Qolayotgan son: $3-2^1=3-2=1\ne 0$

$6)2^0\le 1<2^0$ bundan, $2^0$ni olamiz. Qolayotgan son: $1-2^0=1-1=0$ va jarayon tugadi.

demak, $63_{10}=2^5+2^4+2^3+2^2+2^1+2^0$ tarzida yoyilar ekan va bu sonni pozitsion yoyilma koʻrinishiga oʻtkazamiz

$63_{10}=2^5+2^4+2^3+2^2+2^1+2^0=1\times 2^5+1\times 2^4+1\times 2^3+1\times 2^2+1\times 2^1+1\times 2^0$

va $1\times 2^5+1\times 2^4+1\times 2^3+1\times 2^2+1\times 2^1+1\times 2^0\to 111111_2$

Yaʼni, $63_{10}=111111_2$

Oʻnlik sanoq sistemasidagi nol, boshqa sanoq sistemalarida ham nolga teng, xuddi shuningdek ikkilik sanoq sistemasida ham. Yaʼni, $0_{10}=0_2$

Yana qarang

• Oʻn oltilik sanoq sistemasi
• Sakkizlik sanoq sistemasi
• Rim raqamlari
• Sanoq tizimi